Engineering Mechanics | Equilibrium of Bodies

Equilibrium of Bodies

In the static part when we say that a body is in equilibrium, what we mean is that the body is not moving at all even though there may be forces acting on it. (In general equilibrium means that there is no acceleration i.e., the body is moving with constant velocity but in this special case we take this constant to be zero).

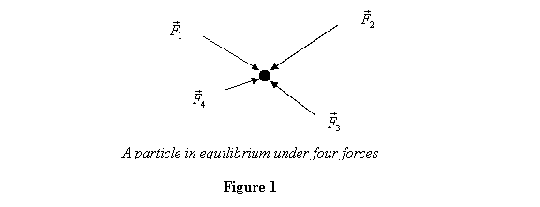
Let us start by observing what all can a force do to a body? One obvious thing it does is to accelerate a body. So if we take a point particle P and apply a force on it, it will accelerate. Thus if we want its acceleration to be zero, the sum of all forces applied on it must vanish. This is the condition for equilibrium of a point particle. So for a point particle the equilibrium condition is

where are the forces applied on the point particle (see figure 13)

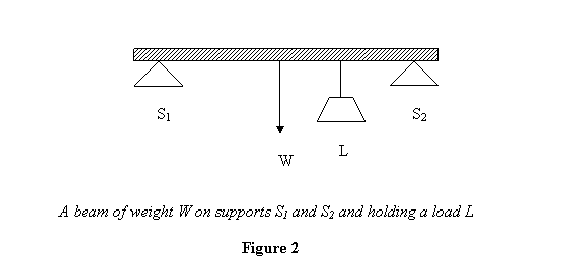
That is all there is to the equilibrium of a point particle. But in engineering problems we deal not with point particles but with extended objects. An example is a beam holding a load as shown in figure 2. The beam is equilibrium under its own weight W , the load L and the forces that the supports S₁and S₂ apply on it.

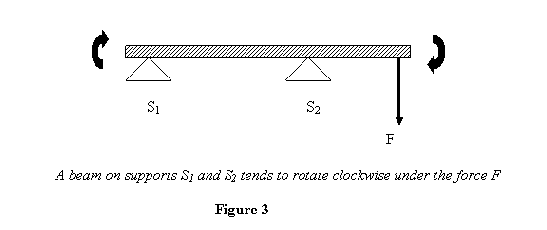
To consider equilibrium of such extended bodies, we need to see the other effects that a force produces on them. In these bodies, in addition to providing acceleration to the body, an applied force has two more effects. One it tends to rotate the body and two it deforms the body. Thus a beam put on two supports S₁ and S₂ tends to rotate clockwise about S₂ when a force F is applied downwards (figure 3).

The strength or ability of a force to rotate the body about a point O is given by the torque generated by it. The torque is defined as the vector product of the displacement vector from O to the point where the force is applied. Thus

This is also known as the moment of the force. Thus in figure 3 above, the torque about S₂ will be given by the distance from the support times the force and its direction will be into the plane of the paper. From the way that the torque is defined, the torque in a given direction tends to rotate the body on which it is applied in the plane perpendicular to the direction of the torque. Further, the direction of rotation is obtained by aligning the thumb of one’s right hand with the direction of the torque; the fingers then show the way that the body tends to rotate (see figure 4). Notice that the torque due to a force will vanish if the force is parallel to .

We now make a subtle point about the tendency of force to rotate a body. It is that even if the net force applied on a body is zero, the torque generated by them may vanish i.e. the forces will not give any acceleration to the body but would tend to rotate it. For example if we apply equal and opposite forces at two ends of a rod, as shown in figure 5, the net force is zero but the rod still has a tendency to rotate. So in considering equilibrium of bodies, we not only have to make sure that the net force is zero but can also that the net torque is also zero.

A third possibility of the action by a force, which we have ignored above, and which is highly explicit in the case of a mass on top of a spring, is that the force also deforms bodies. Thus in the case of a beam under a force, the beam may deform in various ways: it may get compressed, it may get elongated or may bend. A load on top of a spring obviously deforms it by a large amount. In the first case we assume the deformation to be small and therefore negligible i.e., we assume that the internal forces are so strong that they adjust so that there is no deformation by the applied external force. This is known as treating the body as a rigid body. In this course, we are going to assume that all bodies are rigid. So the third kind of action is not considered at all.

So now focus strictly on the equilibrium of rigid bodies: As stated, we are going to assume that internal forces are so great that the body does not deform. The only conditions for equilibrium in them are:

(1)  The body should not accelerate/ should not move which, as discussed earlier, is ensured if that is the sum of all forces acting on it must be zero no matter at what points on the body they are applied. For example consider the beam in figure 2. Let the forces applied by the supports S₁ and S₂ be F₁ and F₂, respectively. Then for equilibrium, it is required that

Assuming the direction towards the top of the page to be y-direction, this translates to

The condition is sufficient to make sure that the net force on the rod is zero. But as we learned earlier, and also our everyday experience tells us that even a zero net force can give rise to a turning of the rod. So F₁ and F₂ must be applied at such points that the net torque on the beam is also zero. This is given below as the second rule for equilibrium.

(2)  Summation of moment of forces about any point in the body is zero i.e. , where is the torque due to the force   about point O. One may ask at this point whether should be taken about many different points or is it sufficient to take it about any one convenient point. The answer is that any one convenient point is sufficient because if condition (1) above is satisfied, i.e. net force on the body is zero then the torque as is independent of point about which it is taken. We will prove it later.

These two conditions are both necessary and sufficient condition for equilibrium. That is all we need to do to achieve equilibrium so in principle solving for equilibrium is quite easy and what we should learn is how to apply these condition efficiently in different engineering situations. We are therefore going to spend time on these topics individually.