Internal energy of a Thermodynamic System
In thermodynamic analysis, the total energy may be divided into two groups: macroscopic and microscopic
The macroscopic forms of energy are those a system possesses as a whole with respect to some outside reference frame, such as kinetic and potential energy.
The microscopic forms of energy are those related to the molecular activity, and they are independent of outside reference frame.
The sum of all the microscopic forms of energy is called the internal energy of the system.
OR
When a certain amount of heat energy is applied to a gas, some of it is converted into mechanical energy and the remaining is stored in the gas itself. The part of energy which is utilized for doing work is known as the external energy of the gas.
Its value is given by
Where PdV represents the work done by the gas.
The part of energy which is stored in the gas and is used for raising its temperature is called the internal energy of the gas.
If (T2 – T1) is the rise in temperature of the gas then the change of its internal energy which is represented by the symbol
per kg of gas.
The “constant” is the same as Cv, i.e. specific heat at constant volume.
Hence, change of internal energy
The above equation always gives the value of 
irrespective of how the gas is heated or expanded.
Internal energy is a property:
A property is any observable characteristic of a system. This implies that during any process the change in the value of a property depends only on the initial and final states; it does not depend on the path of the process.
It also implies that, during a process, if “something” in a system changes in such a way that the amount of the change depends only on the end states, that “something” is a property.
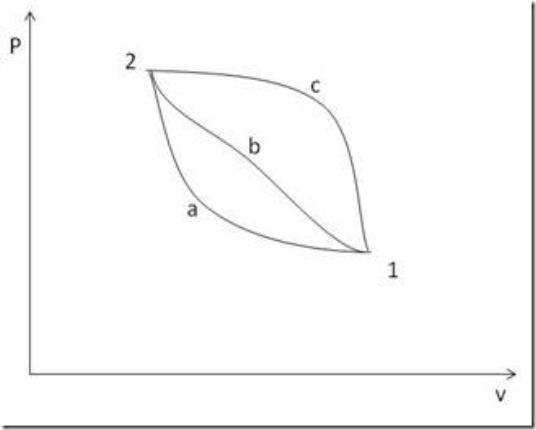
Now consider the condition of a system as represented by point 1 on the Pv-diagram shown in figure below. Let the system first execute a cyclic process 1-a-2-c-1 followed by a second cyclic process 1-b-2-c-1
We know in cyclic process
For the first process
For the second process
From (a) and (b), we have
From the above, it is clear that the integral of (dQ – dW) from state 1 to state 2 is the same for path ‘a’ as for path ‘b’. But all that has been specified about paths ‘a’ and ‘b’ is that they are different.
It follows that
or Q – W has the same value for any path between ‘1’ and ‘2’. But for any process 
so 
; the change of internal energy has same value for any path and depends only on the end state. It follows that U must be a property.
References:
Some my old Notes,
One very old book
Thermodynamics: An Engineering Approach by Cengel and Boles. McGraw Hill Publications