Kinematic Chains, Joints, Degree of Freedom and GRUBLER’S RULE

Kinematic Chains, Joints, Degree of Freedom and GRUBLER’S RULE

KINEMATICS CHAINS

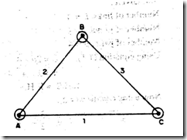
Kinematic chain: A kinematic chain is a group of links either joined together or arranged in a manner that permits them to move relative to one another. If the links are connected in such a way that no motion is possible, it results in a locked chain or structure.

Fig.1.16 Locked chain or structure

 

TYPES OF JOINTS

The usual types of joints in a chain are

•          Binary joint

•          Ternary joint

•          Quaternary joint

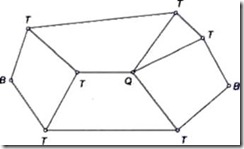
Binary Joint: If two links are joined at the same connection; it is called a binary joint. For example. Fig. 1.17 shows a chain with two binary joints named B.

Ternary Joint: If three links are joined at a connection, it is known as a ternary joint. It is considered equivalent to two binary joints since fixing of any one link constitutes two binary joints with each of the other two links. In Fig. 1.17 ternary links are mentioned as T.

Fig 1.17

Quaternary Joint: If four links are joined at a connection, it is known as a quaternary joint. It is considered equivalent to three binary joints since fixing of any one link constitutes three binary joints. Figure 1.17 shows one quaternary joint.

In general, if ‘n’ number of links are connected at a joint, it is equivalent to (n-1) binary joints.

 

 

DEGREE OF FREEDOM

Degrees of freedom (DOF): It is the number of independent coordinates required to describe the position of a body in space. A free body in space (fig 1.18) can have six degrees of freedom. i.e., linear positions along x, y and z axes and rotational/angular positions with respect to x, y and z axes.

In a kinematic pair, depending on the constraints imposed on the motion, the links may lose some of the six degrees of freedom.

Fig.1.18

Possible Motions:

1.       Three translations along x, y and z axes.

2.       Three rotations about x, y and z axes.

So an object in free space has six degrees of Freedom.

A fixed object has zero degree of freedom.

 

GRUBLER’S RULE

Degrees of freedom/mobility of a mechanism: It is the number of inputs (number of independent coordinates) required to describe the configuration or position of all the links of the mechanism, with respect to the fixed link at any given instant.

Grubler’s equation: Number of degrees of freedom of a mechanism is given by

F = 3(n-1)-2l-h. Where,

F = Degrees of freedom

n = Number of links = n₂ + n₃ +……+n_j, where, n₂ = number of binary links, n₃ = number of ternary links…etc.

l = Number of lower pairs, which is obtained by counting the number of joints. If more than two links are joined together at any point, then, one additional lower pair is to be considered for every additional link.

h = Number of higher pairs

Examples of determination of degrees of freedom of planar mechanisms:

(i)

F = 3(n-1)-2l-h Here, n2 = 4, n = 4, l = 4 and h = 0. F = 3(4-1)-2(4) = 1 I.e., one input to any one link will result in definite motion of all the links.

(ii)

F = 3(n-1)-2l-h Here, n2 = 5, n = 5, l = 5 and h = 0. F = 3(5-1)-2(5) = 2 I.e., two inputs to any two links are required to yield definite motions in all the links.

(iii)

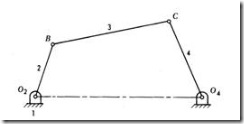
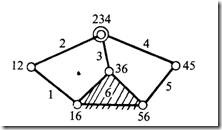
F = 3(n-1)-2l-h Here, n2 = 4, n3 =2, n = 6, l = 7 and h = 0. F = 3(6-1)-2(7) = 1 I.e., one input to any one link will result in definite motion of all the links.

 

 

(iv)

F = 3(n-1)-2l-h Here, n2 = 5, n3 =1, n = 6, l = 7 (at the intersection of 2, 3 and 4, two lower pairs are to be considered) and h = 0. F = 3(6-1)-2(7) = 1

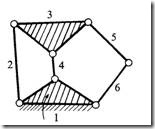
(v)

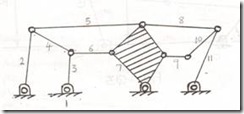
F = 3(n-1)-2l-h Here, n = 11, l = 15 (two lower pairs at the intersection of 3, 4, 6; 2, 4, 5; 5, 7, 8; 8, 10, 11) and h = 0. F = 3(11-1)-2(15) = 0

 

(vi) Determine the mobility of the following mechanisms.

(a)   F = 3(n-1)-2l-h Here, n = 4, l = 5 and h = 0. F = 3(4-1)-2(5) = -1 I.e., it is a structure

(b)   F = 3(n-1)-2l-h Here, n = 3, l = 2 and h = 1. F = 3(3-1)-2(2)-1 = 1

(c)   F = 3(n-1)-2l-h Here, n = 3, l = 2 and h = 1. F = 3(3-1)-2(2)-1 = 1