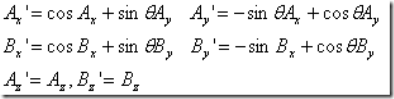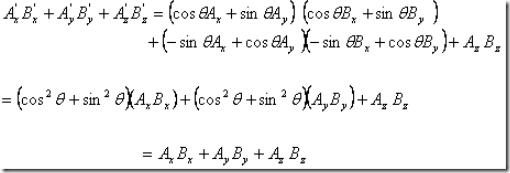Engineering Mechanics | Scalar or Dot Product of Two Vectors

Scalar or dot product:

Now it is easy to show that is a scalar quantity. To show this we calculate this quantity in a rotated frame (rotation could be about the x, y or the z axis) that is obtain and show that it is equal to . As an example we show it for a frame rotated about the z-axis with respect to the other one. In this case

Therefore we get

One can similarly show it for rotations about other axes, which is left as an exercise. This then leads us to define the scalar product of two vectors and as

As shown above this value remain unchanged when view from two different frame-one rotated with respect to the other. Thus it is a scalar quantity and this product is known as the scalar or dot product of two vectors . It is straightforward to see from the definition above that the dot product is commutative that is .

Scalar product of two vectors can also be written in another form involving the magnitudes of these vectors and the angle between them as

where are the magnitudes of the two vectors, and θ is the angle between them. Notice that although can be negative or positive depending on the angle between them. Further, if two non-zero vectors are perpendicular, . From the formula above, it is also apparent that if we take vector to be a unit vector, the dot product   represents the component of in the direction of . Thus the scalar product between two vectors is the product of the magnitude of one vector with the magnitude of the component of the other vector in its direction. Try to see it pictorially yourself. We also write the dot products of the unit vectors along the x, y, and the z axes. These are and .