Engineering Mechanics | Adding and subtracting two vectors (Graphical Method)

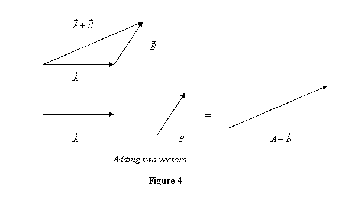
Adding and subtracting two vectors (Graphical Method):

When we add two vectors and by graphical method to get , we take vector , put the tail of on the head of .Then we draw a vector from the tail of to the head of . That vector represents the resultant (Figure 4). I leave it as an exercise for you to show that . In other words, show that vector addition is commutative.

Let us try to understand that it is indeed meaningful to add two vectors like this. Imagine the following situations. Suppose when we hit a ball, we can give it velocity . Now imagine a ball is moving with velocity and you hit it an additional velocity . From experience you know that the ball will now start moving in a direction different from that of . This final direction is the direction of and the magnitude of velocity now is going to be given by the length of .

Now if we add a vector to itself, it is clear from the graphical method that its magnitude is going to be 2 times the magnitude of and the direction is going to remain the same as that of . This is equivalent to multiplying the vector by 2. Similarly if 3 vectors are added we get the resultant . So we have now got the idea of multiplying a vector by a number n . If simply means: add the vector n times and this results in giving a vector in the same direction with a magnitude that n times larger.

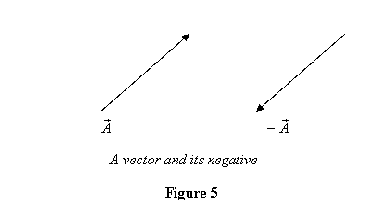
You may now ask: can I multiply by a negative number? The answer is yes. Let us see what happens, for example, when I multiply a vector by -1. Recall from your school mathematics that multiplying by -1 changes the number to the other side of the number line. Thus the number -2 is two steps to the left of 0 whereas the number 2 is two steps to the right. It is exactly the same with vectors. If represents a vector to the right, would represent a vector in the direction opposite i.e. to the left. It is now easy to understand what does the vector represent? It is a vector of the same magnitude as that of but in the direction opposite to it (Figure 5). Having defined , it is now easy to see what is the vector ? It is a vector of magnitude in the direction opposite to .

Having defined , it is now straightforward to subtract one vector from the other. To subtract a vector from , we simply add to that is . Thus to subtract vector from graphically, we add and . This is shown in figure 6.