Seven Questions on Theory of Bending stress
Question.1. Define bending stress.
Answer.
The stress produced to resist the bending moment is called bending stress.
Question.2. Define moment of resistance.
Answer.
The sum of moments of the internal forces about the neutral axis is known as the moment of resistance or flexural strength.
Question.3. Define section modulus.
Answer.
Section modulus is defined as the ratio of moment of inertia of a section about the neutral axis to the distance of the extreme fibre from the neutral axis. It is denoted by the symbol Z. Mathematically, section modulus is given by


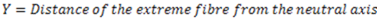
Question.4. Find the section modulus of a circular section whose section diameter is 28 mm.
Answer.
Section modulus, ![]()
Question.5. Explain theory of simple bending.
Answer.
The bending of the beam not accompanied by any shear force is known as pure bending or simple bending.
When a beam of homogeneous material is subjected to equal and opposite couples at its ends, unaccompanied by any shear force, it has uniform bending moment throughout its length, then it is said to be in a state of simple or pure bending.
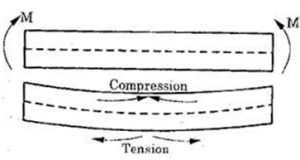
Fig. (a)
Another case of pure or simple bending can be as follows:
Consider a beam ABCD with equal overhangs and supported at B and C, as shown in the Fig. (b). Let a point load W be applied at each of the beam. If we draw the S.F.D. and B.M.D for the given loading, we find that there is no shear force between B and C but the bending moment between B and C is constant.
This means that between B and C, the beam is subjected to a constant bending moment only and no shear force, therefore it is a case of pure bending or simple bending.
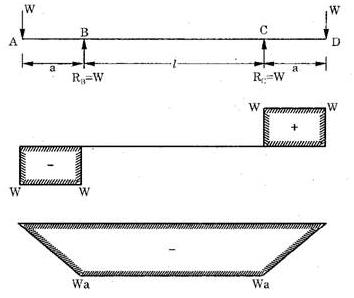
Fig. (b)
Question.6. What assumptions are made in the theory of the simple bending ?
Answer.
The following assumptions are made in the theory of the simple bending:
- A transverse section of the beam, which was a plane before bending is symmetrical about the plane of bending.
- Each cross-section of the beam is symmetrical about the plane of bending.
- The material of the beam is homogeneous (i.e., of the same type throughout) and isotropic (i.e., of the same elastic properties in all directions).
- The beam material is stressed within its elastic limit and obey’s Hooke’s law.
- The value of Young’s modulus of elasticity is the same in tension and compression.
- There is no resultant pull or push across the transverse section of the beam.
- The loads are applied in the plane of bending.
- The radius, of curvature of the beam before bending is very large as compared to the transverse dimensions of the beam.
- Each layer of the beam is free to expand or contract, independently, of the layer, above or below it.
Q.7. Derive the bending equation.
Answer.
Derivation of Bending Equation: Consider a small portion (ABCD) of the beam which is subjected to bending moment M unaccompanied by ant S.F between two parallel sections AB and CD. Let this portion of the beam bend into an arc of a circle with 0 as centre under the effect of applied loads.
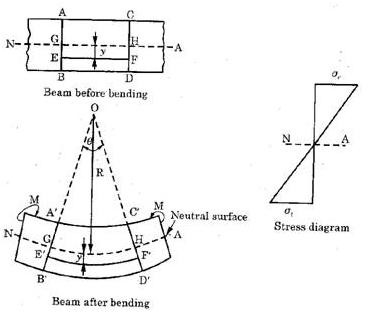
Fig. (c)
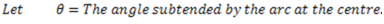
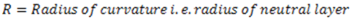
Fibres above neutral axis will be under compression and fibres below neutral axis will be under tension.
Consider a layer EF at a distance ‘y’ from neutral axis. After deformation EF will become 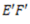 .
.



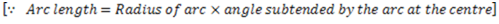



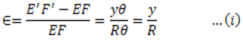
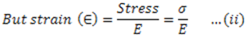
from (i) and (ii)
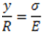
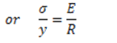
We can also write the above relation as below
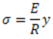
Here. E and R are constants for a given beam. Hence, stress in any fibre is proportional to the distance of the fibre from the neutral axis. Maximum bending stress of opposite nature will be at extreme fibres on both sides of the neutral axis.
Consider elementary areas 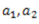 etc. at a distance of
etc. at a distance of 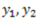 etc. respectively from the neutral axis.
etc. respectively from the neutral axis.

Fig. (d)
Let 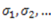 be the stresses on elementary areas
be the stresses on elementary areas  etc.
etc.
Force on elementary area 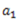 .
.
Force on elementary area 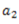 .
.
Moment of all these forces about Neutral-axis,
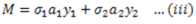
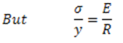
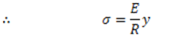
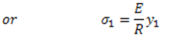
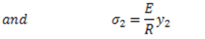
Putting the value of 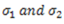 in equation (iii)
in equation (iii)


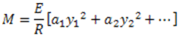
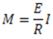
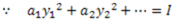
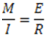
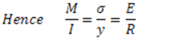
This is known as bending equation.
 .
.
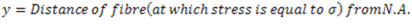
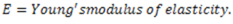
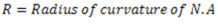
One Response to “Seven Questions on Theory of Bending stress”
s.m.sulakhe
nice to lern hear a good lang. and good explenation