Solved GATE Questions on Fluid kinematics
Question 1. The 2-D flow with velocity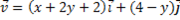 
is
(A) Compressible and irrotational
(B) Compressible and not irrotational
(C) Incompressible and irrotational
(D) Incompressible and not irrotational
GATE-ME-2001
Hint 1. (Ans D)
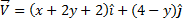
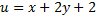
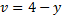
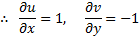
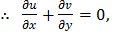hence incompressible.
Again,
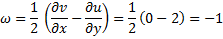
Hence not irrotational.
Question 2. A fluid flow is represented by the velocity field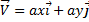 
where a is a constant. The equation of stream line passing through a point (1,2) is
(A) x-2y=0
(B) 2x+y=0
(C) 2x-y=0
(D) x+2y=0
GATE-ME-2004
Hint 2. (Ans C)
Given: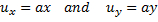 
Equation of stream line is,
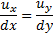
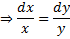
Integrating both sides, we have
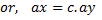
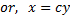
Since the streamline is passed through point (1,2),
Therefore, 1=2c
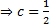
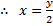
Hence the equation of steam line is, 2x-y=0
Question 3. A leaf is caught in a whirlpool. At a given instant, the leaf is at a distance of 120 m from the centre of the whirlpool. The whirlpool can be described by the following velocity distribution: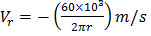 
and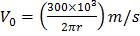 
, where r (in meters) is the distance from the centre of the whirlpool. What will be the distance of the leaf from the centre when it has moved through half a revolution?
(A) 48 m
(B) 64 m
(C) 120 m
(D) 142 m
GATE-ME-2005
Hint 3. (Ans B)
Given Data:
Radial distance (r) =120 m
Radial velocity distribution of leaf, 
Angular velocity distribution of leaf,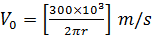 
Let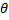 
=Angle turned by the leaf from 0
For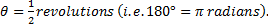 
The radial distance of leaf from centre?
We know , 
Rate of change of radial distance of leaf
Rate of change of angular displacement
Given
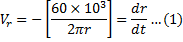
Dividing Equation (1) and Equation (2)
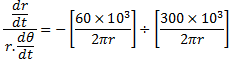
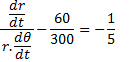
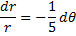
Integrating both sides, we get boundary limits
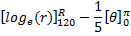
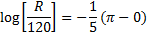
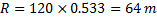
Question 4. The velocity components in the x and y directions of a two dimensional potential flow are u and v, respectively. Then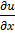 
is equal to
(A)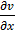 
(B) 
(C)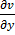 
(D) 
GATE-ME-2005
Hint 4. (Ans D)
For two dimensional flow, continuity equation should be satisfied
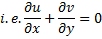
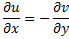
Question 5. A two-dimensional flow field has velocities along the x and y directions given by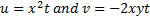 
respectively, where t is time. The equation of streamlines is:
(A)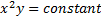 
(B)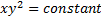 
(C) 
(D) Not possible to determine
GATE-ME-2006
Hint 5. (Ans A)
Given data:
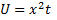
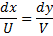
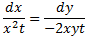
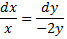
Integrating both sides
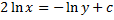
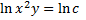
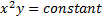
Question 6. In a two dimensional velocity field with velocities u and v along the x and y directions respectively, the convective acceleration along the x direction is given by
(A)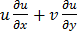 
(B)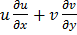 
(C)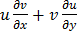 
(D)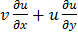 
GATE-ME-2006
Hint 6. (Ans A)
Two dimensional velocity field with velocities u, v and along x and y direction.
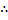Acceleration along x direction, 
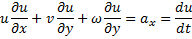
Since, 
for 2- dimensional field, therefore
Convective acceleration=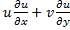
Question 7. Which combination of the following statements about steady incompressible forced vortex flow is correct?
P: Shear stress is zero at all points in the flow.
Q: Vorticity is zero at all points in the flow.
R: Velocity is directly proportional to the radius from the centre of the vortex.
(A) P and Q
(B) R and S
(C) P and R
(D) P and S
GATE-ME-2007
Hint 7. (Ans B)
Statement for Linked Answer Question 8 and 9:
The gap between a moving circular plate and a stationary surface is being continuously reduced, as the circular plate comes down at a uniform speed V towards the stationary bottom surface, as shown in the figure. In the process, the fluid contained between the two plates flows out radially. The fluid is assumed to be incompressible and inviscid.
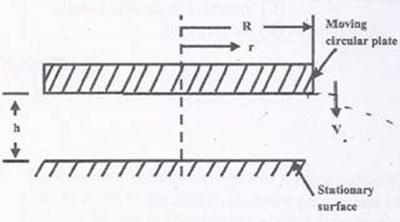
Question 8. The radial velocity 
at any radius r, when the gap width is h, is
(A)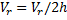 
(B) 
(C) 
(D) 
GATE-ME-2008
Hint 8. (Ans A)
Given Data:
Let V=Downward velocity of circular plate (in m/sec)
R= Radius of circular plate (m)
h= Gap (width) between the moving plate and stationary plate.
.
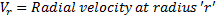According to continuity equation (Law of conservation of mass)
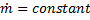
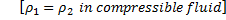
Radial velocity at r=R
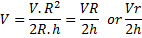
Question 9. The radial component of the fluid acceleration at r=R is
(A)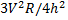 
(B) 
(C) 
(D)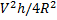 
GATE-ME-2008
Hint 9. (Ans C)
Let 
=Radial component of acceleration at r=R.
According to law of conservation of energy
m (mass flow rate )=constant (c)
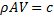
For incompressible fluid
Volume flow rate=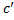
For given instance,
Volume of matter =constant (fixed)
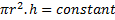
Here r and h are variable. Differentiate w.r.t time (t)
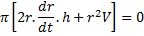
Where V = velocity of circular plate moving down
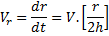
Differentiating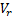 
w.r.t “t”
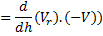
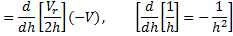
Question 10. For a continuity equation given by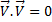 
to be valid, where 
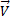is the velocity vector, which one of the following is a necessary condition.?
(A) Steady flow
(B) Irrotational flow
(C) Inviscid flow
(D) Incompressible flow
GATE-ME-2008
Hint 10. (Ans D)
The basic equation of continuity for fluid flow is given by
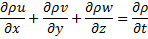
Now if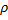 
remains constant, then only we can write
Hence incompressible flow
Question 11. You are asked to evaluate assorted fluid flows for their suitability in a given laboratory application. The following three flow choices, expressed in terms of the two-dimensional velocity fields in the x-y plane, are made available.
P. u=2y, v=-3x
Q. u=3xy, v=0
R. u=-2x, v=2y
Which flows(s) should be recommended when the application requires the flow to be incompressible and irrotational?
(A) P and R
(B) Q
(C) Q and R
(D) R
GATE-ME-2009
Hint 11. (Ans D)
For irrotational flow,
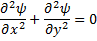
For R :
Now
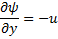
Hence it is irrotational flow.
For P :
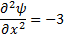
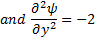
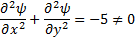
Hence not irrotational
Similarly Q is also not irrotational.
Question 12. A streamline and an equipotential line in a flow field
(A) Are parallel to each other
(B) Are perpendicular to each other
(C) Intersect at an acute angle
(D) An identical.
GATE-ME-2009
Hint 12. (Ans B)
Answer keys
1. (D) 2. (C) 3. (B) 4. (D) 5. (A) 6. (A) 7. (B) 8. (A) 9. (c) 10.(D) 11.(D) 12.(B)