Solved GATE Questions on Conduction
Question 1. Consider steady-state heat conduction across the thickness in a plane composite wall (as shown in the figure) exposed to convection conditions on both sides.
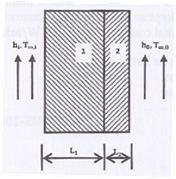
Given : 
; 
; 
; 
; 
; 
.
Assuming negligible contact resistance between the wall surfaces, the interface temperature , in T(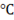
), of the two walls will be
(A)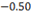 
(B) 
(C)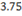 
(D)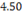 
GATE-ME-2009
Hint 1. (Ans C)
Now
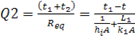
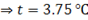
Alternately
Under steady state conditions
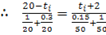
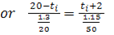
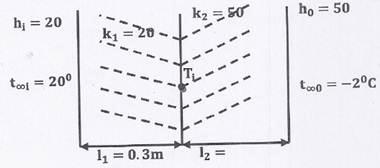
Question 2. A fin has 5 mm diameter and 100 mm length. The thermal conductivity of fin material is 400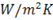 
. One end of the fin is maintained at 130
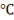and its remaining surface is exposed toambient air at 30
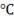. If the convective heat transfer coefficient is 40 W/
, the heat loss (in W) from the fin is
(A) 0.08
(B) 5.0
(C) 7.0
(D) 7.8
GATE-ME-2010
Hint 2. (Ans B)
Question 3. A pipe of 25 mm diameter carries steam. The heat transfer coefficient between the cylinder and surrounding is 5 W/
. It is proposed to reduce the heat loss from the pipe by adding insulation having a thermal conductivity of 0.05 W/mK. Which one of the following statements are True?
(A) The outer radius of the pipe is equal to the critical radius.
(B) The outer radius of the pipe is less than the critical radius.
C) Adding the insulation will reduce the heat loss.
(D) Adding the insulation will increase the heat loss.
GATE-ME-2011
Hint 3. (Ans C)
addition of insulation will reduce heat loss.
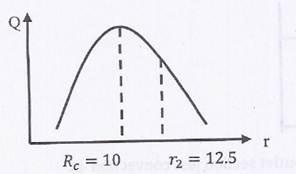
Question 4. Consider one-dimensional steady state heat conduction, without heat generation, in a plane wall; with boundary conditions as shown in the figure below. The conductivity of the wall is given by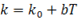 
where 
and b are positive constants, and T is temperature.
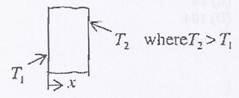
will
(A) Remain constant
(B) Be zero
(C) Increase
(D) Decrease
GATE-ME-2013
Hint 4. (Ans D)
As x increases, T increases from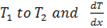 
decreases.
Question 5. Consider one-dimensional steady state heat conduction along x-axis(
), through a plane wall with the boundary surface (x=0 and x=L) maintained at temperatures of 0
and 100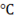
. Heat is generated uniformly throughout the wall. Choose the correct statement.
(A) The direction of heat transfer will be from the surface at 100
to the surface at 0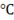
.
(B) The maximum temperature inside the wall must be greater than 10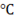
.
(C) The temperature distribution is linear with in the wall.
(D) The temperature distribution is symmetric about the mid-plane of the wall.
GATE-ME-2013
Hint 5. (Ans B)
General profile is
Question 6. A steel ball of diameter 60 mm is initially in thermal equilibrium at 1030
in a furnace. It is suddenly removed from the furnace and cooled in ambient air at 30
, with convective heat transfer coefficient h=20
. The thermo-physical properties of steel are ; density 
, conductivity k=40W/mK and specific heat c=600 J/kgK. The time required in seconds to cool the steel ball in air from 1030 
to 430 
is
(A) 519
(B) 931
(C) 1195
(D) 2144
GATE-ME-2013
Hint 6. (Ans D)
Lumped analysis
Apply log,
Common data for Question 7 and 8
Water (Specific heat,
) enters a pipe at a rate of 0.01 kg/s and a temperature of 20
. The pipe , of diameter 50 mm and length 3m, is subjected to a wall heat flux 
in 
.
GATE-ME-2013
Question 7. If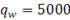 
and the convection heat transfer coefficient at the pipe outlet is 1000
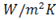, the temperature in 
at the inner surface of the pipe at the outlet is
(A) 71
(B) 76
(C) 79
(D) 81
Hint 7 (Ans D)
Convection does not matter as we take outlet section just convection in
Where 
wall temperature at the outlet
Where h=heat transfer coefficient at the pipe outlet=76+5=81
Question 8. If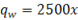 
, where 
is in meter and in the direction of flow (
at the inlet), the bulk mean temperature of the water leaving the pipe in 
is
(A) 42
(B) 62
(C) 74
(D) 104
Hint 8. (Ans B)
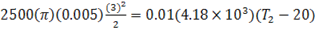
Answer Keys
1. (C) 2. (B) 3. (C) 4. (D) 5. (B) 6. (D) 7. (D) 8. (B)