Eight Questions on Moment of Inertia
Question.1. Define moment of inertia.
Answer.
Moment of inertia of a mass about any reference axis is the second moment of the mass about hat axis.
Moment of inertia is also termed as the second moment of mass and is denoted by I.
![]()

Question.2. What do u mean by second moment of area?
Answer.
The product of the area and the square of the distance of the C.G. of the area from that axis is known as second moment of area. It is called second moment of area because we are taking moment of area about an axis twice.

Question.3. Define radius of gyration.
Answer.
The distance of a point where the whole area of a body is assumed to be concentrated from a given axis is called radius of gyration.
Question.4. State theorem of parallel axis.
Answer.
It states that the moment of Inertia of a lamina about any axis in the plane of the lamina is equal to the sum of the Moment of Inertia of that lamina about its centroidal axis parallel to the given axis and the product of the area of the lamina and the square of the perpendicular distance between the two axis.
Question.5. State theorem of perpendicular axis.
Answer.
The perpendicular axis theorem states that the moment of inertia of a plane figure about an axis perpendicular to the figure and passing through the centroid is equal to the sum of moment of inertia of the given figure about two mutually perpendicular axis passing through the centroid and lying in the plane of the given figure.
Question.6. State and prove theorem of parallel axis.
Answer.
It states that the moment of inertia of a lamina about any axis in the plane of the lamina is equal to the sum of the Moment of Inertia of that lamina about its centroidal axis parallel to the given axis and the product of the area of the lamina and square of the perpendicular distance between the two axis.
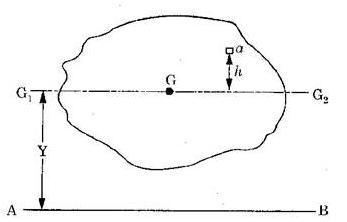
Fig.(a) Theorem of Parallel Axis
Proof. Consider an elemental area 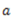 at a distance
at a distance 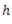 from the line
from the line  . Moment of inertia of the area
. Moment of inertia of the area  about AB is given by
about AB is given by
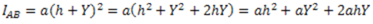
The moment of inertia of the whole lamina about AB is given by

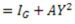



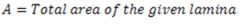

Question.7. State and prove theorem of perpendicular axis.
Answer.
The perpendicular axis theorem states that the moment of inertia of a plane figure about an axis perpendicular to the figure and passing through the centroid is equal to the sum of moment of inertia of the given figure about two mutually perpendicular axis passing through the centroid and lying in the given figure.
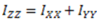
Where X-X and Y-Y are two mutually perpendicular axis in the plane of the lamina and Z-Z is an axis passing through the centroid and perpendicular to the plane of the lamina.
Z-Z axis is called polar axis and 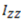 is known as the polar moment of inertia. Polar moment of inertia is also denoted as
is known as the polar moment of inertia. Polar moment of inertia is also denoted as 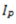 .
.
Proof : Consider a small lamina (P) of area 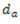 having co-ordinates as X and Y along two mutually perpendicular OX and OY on a plane section as shown in fig.
having co-ordinates as X and Y along two mutually perpendicular OX and OY on a plane section as shown in fig.
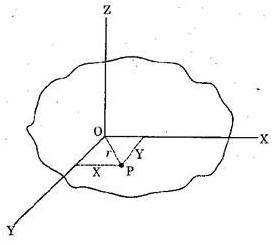
Fig. (b) Theorem of Perpendicular Axis
Now consider an axis OZ perpendicular to OX and OY. Let (r) be the distance of the lamina (P) from Z-Z axis such that 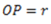 .
.
From the geometry of the Fig. (b):
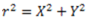
But MOI of the lamina P about X-X axis
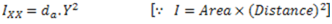

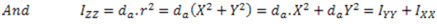
Question.8. Give equation for the following by explaining each term used in that equation :-
1.Moment of inertia of a rectangular section.
2.Moment of inertia of a triangular section about an axis passing through its centroid and parallel to base.
3. Moment of inertia of circular section.
Ans. (1)
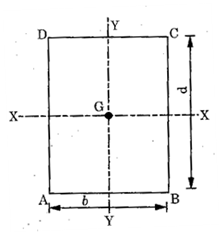
Fig. (c) Moment of Inertia of a rectangular section
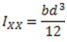
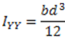
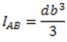



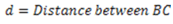
(2)
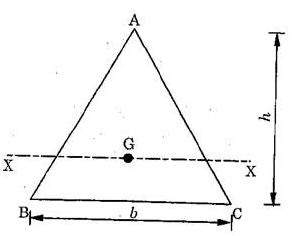
Fig. (d) Moment of Inertia of the triangular section about an axis passing through its centroid and parallel to base
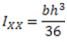

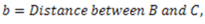

(3)
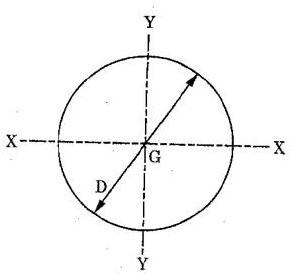
Fig. (e) Moment of Inertia of a circular section
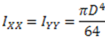



One Response to “Eight Questions on Moment of Inertia”
Abhisek
Very good & important questions in a very brief format