Eight Questions on Balancing
Question.1. Define balancing.
Answer.
Balancing is a method of correcting or eliminating unwanted inertia forces and couples in rotating and reciprocating parts of the machine.
Question.2. Define static balance.
Answer.
A system of rotating masses is said to be in static balance if the centre of gravity of the system of masses lie on the axis of rotation.
Question.3. Define dynamic balance.
Answer.
A system of rotating masses is said to be in dynamic balance if any resultant centrifugal force or couple does not exist.
Question.4. Define reference plane.
Answer.
When several masses rotating in different planes are transferred to a single plane, then this single plane is known as the reference plane.
Question.5. Explain the method of balancing a single rotating mass by another rotating mass in same plane.
Answer.
When a certain mass is connected to a rotating shaft, it will exert some centrifugal force. The tendency of this centrifugal force is to bend the shaft and to produce vibrations in it. To prevent the effect of the unbalanced centrifugal force, another mass is connected to the opposite side of the shaft at such a position so that the effect of the centrifugal force due to first mass can be balanced.
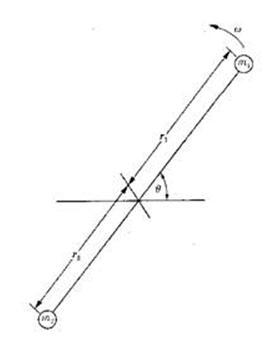
Fig. Balancing of a Single Rotating Mass by Another Rotating Mass in the Same Plane
Let us consider a mass 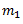 connected to a shaft as shown in the Fig.
connected to a shaft as shown in the Fig.
Let
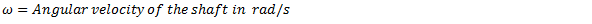

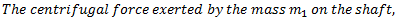
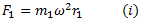
The force acts radially outwards and continuously changes its direction. To counteract this force, a balance mass 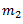 is introduced at a distance
is introduced at a distance  from the axis of the shaft in the same plane of the disturbing force
from the axis of the shaft in the same plane of the disturbing force  such that centrifugal force of the two masses are equal and opposite.
such that centrifugal force of the two masses are equal and opposite.
Let 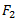 be the centrifugal force due to balance mass
be the centrifugal force due to balance mass 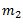 .
.
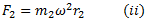
For complete balance,

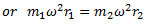

The product 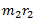 may be split in any convenient way. Normally,
may be split in any convenient way. Normally, 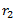 is kept large to reduce
is kept large to reduce 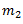 .
.
Question.6. Explain the method of balancing a number of masses rotating in one plane by another mass rotating in the same plane.
Answer.
Let us consider four masses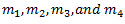 attached rigidly to the shaft rotating at angular speed
attached rigidly to the shaft rotating at angular speed 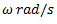 as shown in Fig. (a). Let
as shown in Fig. (a). Let 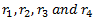 are the distances of
are the distances of 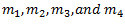 from the axis of rotating shaft.
from the axis of rotating shaft.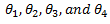 are the angles of masses
are the angles of masses 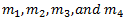 with the X-axis.
with the X-axis.
The centrifugal force for each mass is proportional to the product of mass and its radius of rotation as 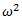 is same for each mass. All these forces are acting radially outwards and form a system of concurrent coplanar forces at point O i.e. on the axis of rotation. The resultant of all such forces can be found by the following two methods:
is same for each mass. All these forces are acting radially outwards and form a system of concurrent coplanar forces at point O i.e. on the axis of rotation. The resultant of all such forces can be found by the following two methods:
1. Analytical method,
2. Graphical Method.
(a) Space Diagram (b) Vector Diagram
Fig. Balancing of a Number of Masses Rotating in One Plane by Another Mass Rotating in the Same Plane
1. Analytical method :
(i) Resolve each force horizontally and vertically.
(ii) Find the resultant horizontal component (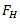 ) of the centrifugal forces which is
) of the centrifugal forces which is

(iii) Similarly, find the resultant vertical (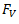 ) of the centrifugal forces which is
) of the centrifugal forces which is
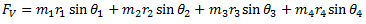
(iv) Find the magnitude of the resultant centrifugal force.
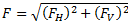
(v) Find the direction of the resultant centrifugal force.

Where 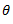 is the angle made by the resultant force with X-axis.
is the angle made by the resultant force with X-axis.
(vi) The balancing and the resultant forces are equal and opposite to each other.
(vii) Find the magnitude of the balancing mass from the relation,
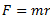
2. Graphical Method : The analytical method is lengthy procedure and also there is possibility of mistake in the calculations. Therefore, graphical is generally preferred. The steps followed in the graphical method are as follows:
(i) Draw the space diagram as shown in fig. (a).
(ii) Draw the vector diagram as shown in fig. (b) in such a way that ‘ab’ represents the centrifugal force due to mass 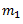 which is equal to
which is equal to 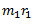 . Magnitude and direction is drawn on some suitable scale. Similarly bc, cd and de are drawn to represent centrifugal forces due to masses
. Magnitude and direction is drawn on some suitable scale. Similarly bc, cd and de are drawn to represent centrifugal forces due to masses 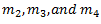 .
.
(iii) The resultant force is shown by the closing side ‘ae'(dotted line).
(iv) The balancing force is equal and opposite to the resultant force.
(v) Find the magnitude of the balancing mass m such that
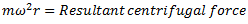
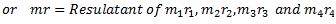
Question.7. Explain the method of balancing a number of masses rotating in different planes.
Answer.
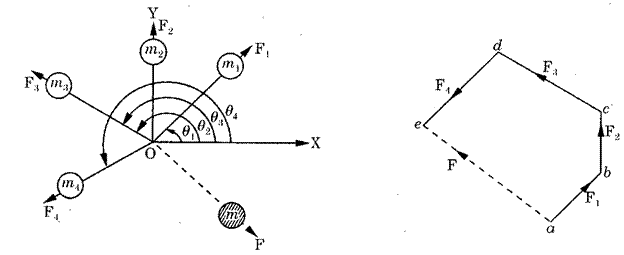
Let us consider four masses 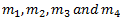 rotating in four different planes
rotating in four different planes 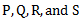 at different radii respectively as shown in fig. Let us consider that all the above four masses are attached to a single rotor rotating with angular velocity
at different radii respectively as shown in fig. Let us consider that all the above four masses are attached to a single rotor rotating with angular velocity 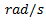 . Let the distance of planes
. Let the distance of planes 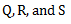 from the plane
from the plane 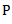 are
are 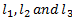 respectively.
respectively.

Fig. Balancing of a Number of Masses Rotating in Different Planes
Let us consider the plane P as reference plane. Now, if we transfer the masses 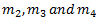 rotating in planes
rotating in planes 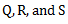 to the reference plane
to the reference plane 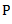 , then there will occur four unbalanced forces
, then there will occur four unbalanced forces 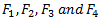 and three unbalanced couples
and three unbalanced couples 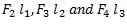 in the reference plane. For complete balancing of the system, the following two conditions must be satisfied:
in the reference plane. For complete balancing of the system, the following two conditions must be satisfied:
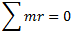
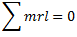
It should be noted that the distances of planes to the left side of reference plane are taken as negative, while to the right side as positive.
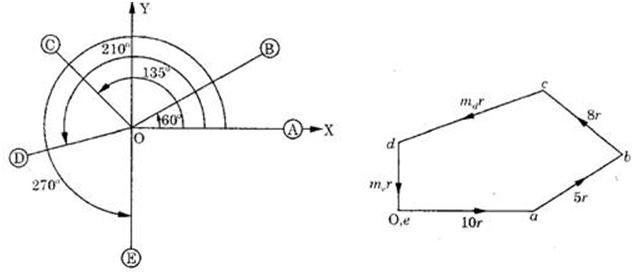
Question.8. Five masses A,B,C,D and E rotate in the same plane at equal radii. The masses A, B and C are 10 kg, 5 kg, and 8 kg respectively. The angular position of masses B, C, D and E measured in the same direction from A are 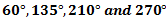 respectively. Find the masses D and E for complete balance.
respectively. Find the masses D and E for complete balance.
Answer.
![]()
Graphical Method:
|
Component |
Mass(m) (kg) |
Radius(r)(m) |
mr(kgm) |
|
|
10 |
r |
10r |
|
|
5 |
r |
5r |
|
|
8 |
r |
8r |
|
|
|
r |
|
|
|
|
r |
|
(a) Space Diagram (b) Vector Diagram (Force Polygon)
From the tabular data and statement of the problem, it is clear that the system is in complete balance. Therefore, the force polygon should be a closed one. Hence it is drawn with the help of data in column 4 of the table as under:
1. Draw a line 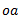 parallel to
parallel to 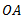 and equal to
and equal to  or some suitable scale.
or some suitable scale.
2. From point 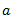 , draw line
, draw line  parallel to
parallel to 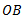 and equal to
and equal to 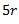 .
.
3. Similarly, draw line 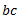 parallel to
parallel to  and equal to
and equal to  .
.
4 From point c, draw line 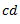 parallel to
parallel to 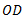 .
.
5. From point O, draw line 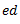 parallel to
parallel to 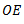 to cut line
to cut line 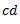 at point
at point  .
.
6. Measure 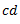 and equate it to
and equate it to 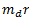 to find the value of
to find the value of 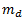 .
.
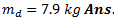
7. Similarly, measure 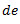 and equate it to
and equate it to 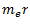 . Find the value of
. Find the value of 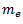 .
.
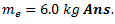
Let us now solve the above problem by analytical method.
Analytical Method: 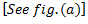
|
Component |
Mass (m)(kg) |
Radius (r) (m) |
|
|
|
|
|
10 |
|
|
|
0 |
|
|
5 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
For complete balance,

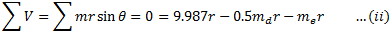
From equation (i),


From equation (ii),
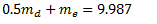
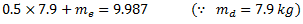
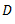
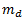
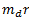
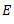

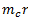
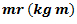
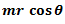
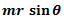

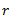
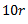
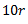

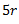
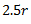
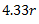
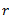
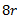
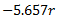

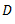
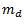
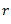
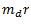
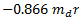

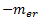
3 Responses to “Eight Questions on Balancing”
firdous patait
I clearly understand about rotating masses…
Sugumar
Excellent, informative,
Ahmed Abdullah
May I ask about an example in real life show the balancing of single mass rotating by another single mass rotating in the same plane???