Second Law of Thermodynamics with Detailed Explanation

 Introduction to Second Law of Thermodynamics:

The second law of thermodynamics may be written in several ways. Regardless of the terminology used, however, the purpose of second law is to give a sense of direction to the energy transfer. This, combined with the first law gives us the information necessary to analyse energy-transfer process.

One of the statements of second law reads:

Whenever energy is transferred, the level of energy cannot be conserved and some energy must be permanently reduced to a lower level.

When the above statement is combined with first law of thermodynamics (the law of energy conservation), the following results:

Whenever energy is transferred, energy must be conserved but the level of energy cannot be conserved and some energy must be permanently reduced to a lower level.

So what is energy level?

Let us consider two identical blocks of material at different temperatures T₁ and T₂ (say T₁ = 1000K and T₂ = 500K). The block at 1000 K has higher thermal energy level than the one at 500K. The internal energy of the blocks are

If these blocks are brought together and reach thermal equilibrium at temperature T₃, then the energy of the two blocks is

However, by the first law

Thus the final temperature is less than one of the initial temperatures. We assume the energy level to be proportional to temperature, so we see that there has been an energy level decrease.

There has also been an energy level increase, but the second law states that there will only be a decrease. The energy level finally is less than the highest energy level initially. Note that the total energy of either block has nothing to do with the energy level. The mass of block 2 could be 10 times larger than that of block 1, but there will be an energy level decrease. In such a case we will find T₃ = 545.5K.

Actually, the energy level is more than the temperature level of a system. A block of material of a small mass at a distance above a zero datum would have a higher energy level than a block of large mass of the same material resting at a zero datum.

In this case the energy level is indicated by the potential energy.

The potential energy of the small mass is greater than that of the larger mass. The energy level is a function of all thermodynamic forces in a system that will cause energy transfer from the system. The energy level of the system is lowered when the values of these thermodynamic forces with the system decrease.

The direction of energy transport is from a higher energy level to a lower energy level.

Second law for a Cycle:

As with all thermodynamic laws, there is no way to mathematically prove the second law. Carnot first observed that in steam engines, there could be no work produced unless there was heat flow from a higher temperature reservoir to a low temperature reservoir. He further noted that the work produced was a function of the temperature difference between the reservoirs and was greater for a greater temperature difference.

Kelvin-Planck’s Statement:

It is impossible to construct an engine working on cyclic process whose sole purpose is to convert all the heat supplied to it into equivalent amount of work.

In other words, no heat engine converts, or can convert, more than a small fraction of the heat supplied to it, into work; a large part is necessarily rejected as heat.

The ratio

is thus a fraction always much less than unity. This fraction is called thermal efficiency of the engine. In other words, thermal efficiency of an engine is always less than unity.

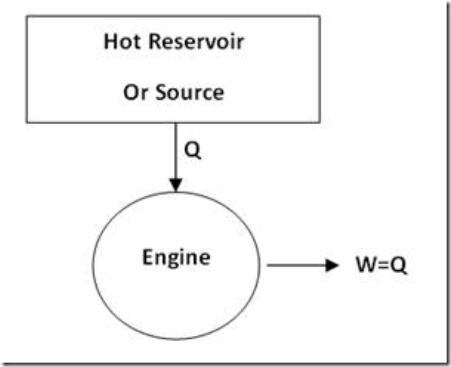
Thus according to this statement of Second Law of Thermodynamics, an engine working on cyclic process cannot receive heat Q from a heat source and deliver work W equal to Q (When W and Q are both expressed in the same units) as shown in figure 1.

Figure 1: Practically impossible Engine

It may be noted that First Law of Thermodynamics does not put any restriction as to the fraction of heat drawn from a heat source, for its conversion into work.

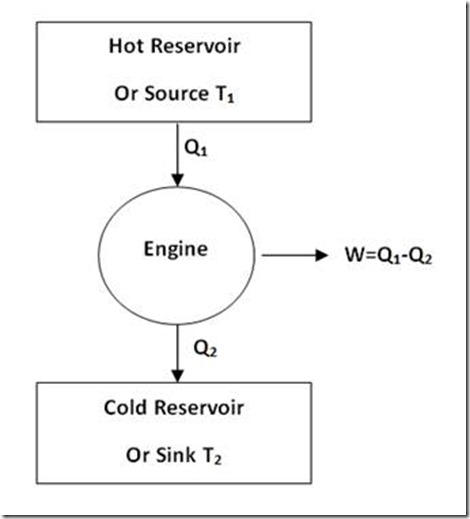
So, such an engine will, of course, not violate First Law of Thermodynamics. But it is not possible to have such a 100% efficient engine in view of the limitation expressed by Second Law of Thermodynamics according to which a part of the heat drawn from heat source (at higher temperature) must be rejected to a low temperature reservoir (sink). Therefore, for an engine to continuously convert heat energy into useful work, two heat reservoirs are an essential minimum as shown in figure 2.

Figure 2: Practically possible Engine

Clausius’ Statement:

Heat flows from a hot object to a cold object unaided but it cannot flow from a cold object to a hotter object without the expenditure of mechanical energy.

From the above statement it follows that a body can only absorb heat from a source which has its temperature higher than that of the body itself. If it is required to lower the temperature of the body to below that of its surroundings, mechanical energy will have to be spent to do so. The example of the application of this law is found in a refrigeration system.

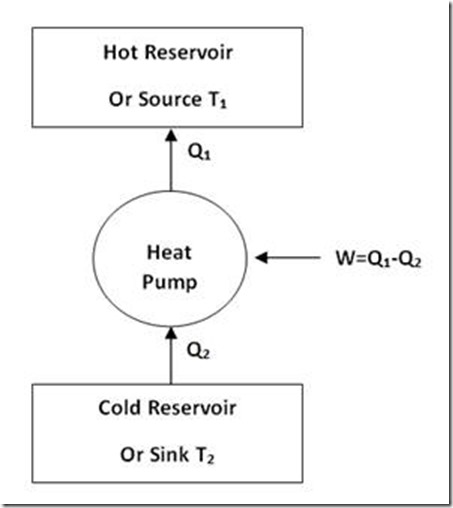
This is further explained in figure 3.

Figure 3

If a hot reservoir (heat source) is at a temperature T₁ and a cold reservoir (heat sink) is at a temperature T₂, then according to Calusius statement, heat cannot flow from heat sink to heat source without the aid of an external agency like a heat pump which takes mechanical work to deliver heat continuously from lower temperature T₂ to higher temperature T₁.

Reversible and Irreversible Processes:

A process is said to be reversible if the reversal of the process does not leave any trace on the system and the surroundings (universe). For example, during a process from state 1 to state 2, let the work transfer be W₁₂ and the heat transfer be Q₁₂. If by supplying back W₁₂ and Q₁₂ to the system, the state can be changed back from 2 to 1, the process is said to be reversible.

If there is any change in the requirement of work and heat to bring back the system from state 2 to 2, the process becomes irreversible. In certain processes like mixing neither work nor heat exchange may take place during the forward process of mixing. If it is possible to separate the components of such mixture without any energy input at all, such a process will be reversible. But practically all mixing processes are irreversible, as a spontaneous separation is impossible.

In practice, most of the processes are irreversible to some degree. The causes of irreversibility are:

• a. Mechanical and Fluid Friction
• b. Unrestricted expansion or unrestricted fall
• c. Heat transfer with a finite temperature difference and
• d. Mixing

Mechanical friction converts work into heat. This heat cannot supply back the same amount of work as was consumed for its production. Friction between the fluid molecules converts kinetic energy into heat. This heat also cannot be completely converted back into kinetic energy. So, fluid friction also causes irreversibility.

Unrestricted expansion (free expansion) also involves fluid friction and is irreversible. During the free expansion, work is not done, but the pressure is reduced. In order to recompress the medium, work is required. Thus free expansion becomes irreversible.

Whenever heat is transferred with finite temperature difference, it involves irreversibility as the heat so transferred cannot spontaneously flow back against the temperature gradient.

Finally, two fluids can spontaneously mix with each other (say nitrogen and oxygen). But once mixed, the components cannot be separated without energy input, thus causing irreversibility, due to mixing.

A cycle will be reversible if all the processes constituting the cycle are reversible. Reversible processes and cycles are the ideals with which actual cycles and processes are compared, in the attempt to improve the working of devices.

Carnot Theorem (Corollaries of the second law):

There are two corollaries of the Second Law.

The first one:

It is impossible to construct an engine to operate between two heat reservoirs, each having a fixed and uniform temperature, which will exceed the efficiency of a reversible engine operating between the same reservoirs.

Figure 4 explains such a situation. Note that the reversible engine is a Carnot Engine, whereas the other engine may have irreversibilities associated with it.

Figure 4: Reversible and irreversible engines operating between the same temperature limits

Assume that the irreversible engine has efficiency greater than that of the reversible engine. Let W₁ be the work produced by the irreversible engine, while receiving heat Q₁, and let W_R be the work produced by the reversible engine (Carnot) when receiving the same amount of heat Q₁. The assumption tells us that W₁ > W_R.

Now, run the reversible engine as a reversed Carnot Engine so that it will supply the amount of heat Q₁ to the high temperature reservoir. It would be possible to run the reversible engine by supplying work from the irreversible engine and still have some net work remaining. This is a perpetual motion machine of the second kind and cannot exist because it violates the second law of thermodynamics. Thus the assumption that W₁ > W_R is not valid and the first corollary must be valid.

The second corollary follows:

All reversible engines have the same efficiency when working between the same two constant temperature heat reservoirs.

The proof of the proposition follows that of the previous one. Assume that the proposition is not true in a particular case, and then show that a perpetual motion machine of the second kind is a consequence. In this case, the irreversible engine is replaced by a Carnot engine of higher efficiency than the other reversible engine.

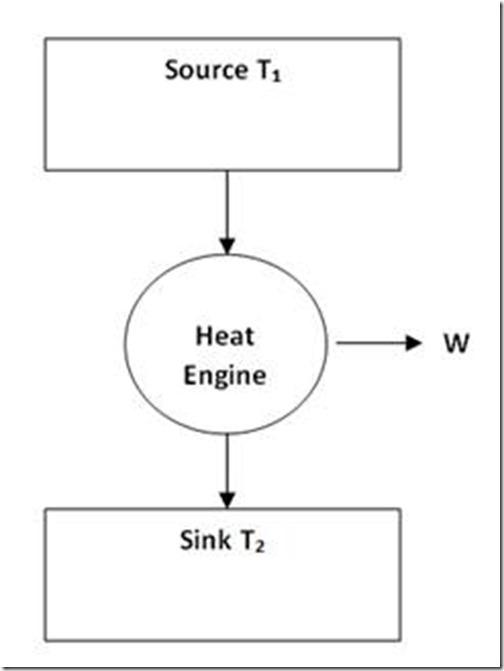
Heat engine is a mechanical device which converts heat energy into mechanical energy. Let us consider a source of temperature T₁ and a sink at temperature T₂ used for the purpose. Heat is drawn from the source and is converted. The balance of heat is rejected to the sink (as given in figure 5).

Figure 5

Let heat supplied to the heat engine be Q₁ kJ. Let heat rejected to the sink be Q₂ kJ.

Net work transfer = (Q₁ – Q₂) kJ

Efficiency of the heat engine would be

Let us imagine the operations reversed. i.e. Let the engine receive heat from sink at lower temperature and pump the heat into source at higher temperature. This is against nature and it is not possible. Hence, the machine consumed energy in the form of work transfer to perform this operation. The ratio is known as coefficient of performance. The machine is a reverted heat engine. It is also called refrigerator. This forms the basis of second law of Thermodynamics.

The law states:

It is impossible to construct a device to work in a cyclic process whose sole effect is the transfer of heat from a system at a lower temperature to a system at higher temperature.

Another form of the statement:

It is impossible for heat energy to flow from a body or a system at a lower temperature to a body or system at a higher temperature without aid of external work.

Third statement of Second Law of Thermodynamics:

It is impossible to convert all the heat energy supplied to a heat engine without rejecting a portion to the sink.

References:

Some of my old notes,
An unknown book from my student life 🙂