Cam nomenclature & Displacement Diagram for Different CAM Profiles

Cam nomenclature & Displacement Diagram for Different CAM Profiles

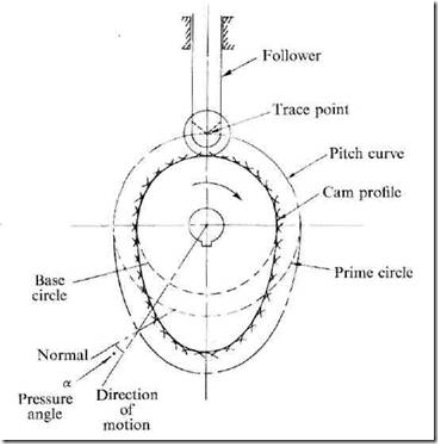
Fig. :Cam nomenclature

Cam Profile: The contour of the working surface of the cam.

Tracer Point: The point at the knife edge of a follower, or the center of a roller, or the center of a spherical face.

Pitch Curve: The path of the tracer point.

Base Circle: The smallest circle drawn, tangential to the cam profile, with its center on the axis of the camshaft. The size of the base circle determines the size of the cam.

Prime Circle: The smallest circle drawn, tangential to the pitch curve, with its center on the axis of the camshaft.

Pressure Angle: The angle between the normal to the pitch curve and the direction of motion of the follower at the point of contact.

Types of follower motion:

Cam follower systems are designed to achieve a desired oscillatory motion. Appropriate displacement patterns are to be selected for this purpose, before designing the cam surface. The cam is assumed to rotate at a constant speed and the follower raises, dwells, returns to its original position and dwells again through specified angles of rotation of the cam, during each revolution of the cam.

Some of the standard follower motions are as follows:

They are, follower motion with,

(a) Uniform velocity

(b) Modified uniform velocity

(c) Uniform acceleration and deceleration

(d) Simple harmonic motion

(e) Cycloidal motion

Displacement diagrams: In a cam follower system, the motion of the follower is very important. Its displacement can be plotted against the angular displacement θ of the cam and it is called as the displacement diagram. The displacement of the follower is plotted along the y-axis and angular displacement θ of the cam is plotted along x-axis. From the displacement diagram, velocity and acceleration of the follower can also be plotted for different angular displacements θ of the cam. The displacement, velocity and acceleration diagrams are plotted for one cycle of operation i.e., one rotation of the cam. Displacement diagrams are basic requirements for the construction of cam profiles. Construction of displacement diagrams and calculation of velocities and accelerations of followers with different types of motions are discussed in the following sections.

(a) Follower motion with Uniform velocity:

Fig.2 shows the displacement, velocity and acceleration patterns of a follower having uniform velocity type of motion. Since the follower moves with constant velocity, during rise and fall, the displacement varies linearly with θ. Also, since the velocity changes from zero to a finite value, within no time, theoretically, the acceleration becomes infinite at the beginning and end of rise and fall.

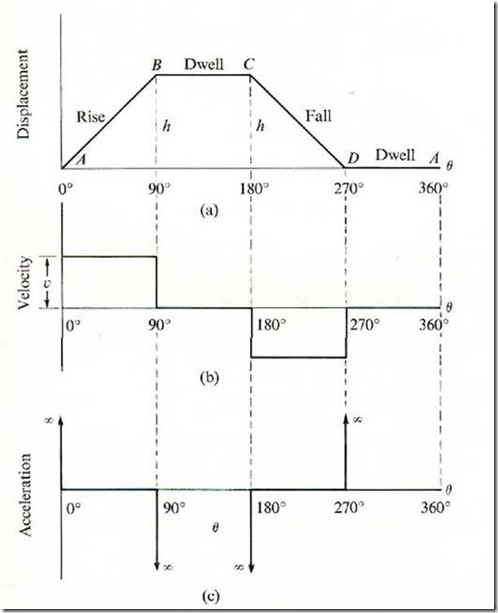Fig.2: Follower motion with Uniform velocity

(b) Follower motion with modified uniform velocity:

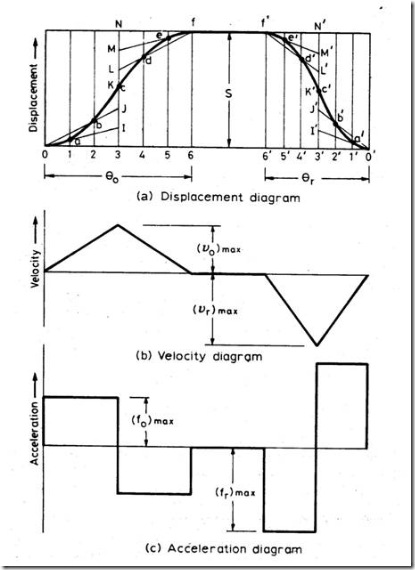
It is observed in the displacement diagrams of the follower with uniform velocity that the acceleration of the follower becomes infinite at the beginning and ending of rise and return strokes. In order to prevent this, the displacement diagrams are slightly modified. In the modified form, the velocity of the follower changes uniformly during the beginning and end of each stroke. Accordingly, the displacement of the follower varies parabolically during these periods. With this modification, the acceleration becomes constant during these periods, instead of being infinite as in the uniform velocity type of motion. The displacement, velocity and acceleration patterns are shown in fig. 3.

fig.3: Follower motion with modified uniform velocity

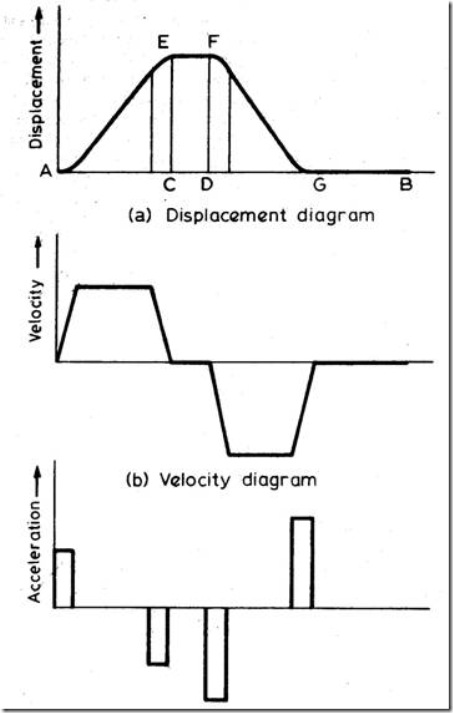
(c) Follower motion with uniform acceleration and retardation (UARM):

Here, the displacement of the follower varies parabolically with respect to angular displacement of cam. Accordingly, the velocity of the follower varies uniformly with respect to angular displacement of cam. The acceleration/retardation of the follower becomes constant accordingly. The displacement, velocity and acceleration patterns are shown in fig. 4.

Fig.4: Follower motion with uniform acceleration and retardation

s = Stroke of the follower

θ_o and θ_r = Angular displacement of the cam during outstroke and return stroke.

ω = Angular velocity of cam.

Time required for follower outstroke = t_o =

Time required for follower return stroke = t_r =

Average velocity of follower =

Average velocity of follower during outstroke =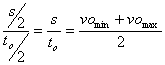

 

vo_min = 0

= Max. velocity during outstroke.

 

Average velocity of follower during return stroke =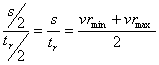

 

vr_min = 0

 

= Max. velocity during return stroke.

Acceleration of the follower during outstroke =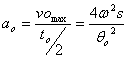

 

Similarly acceleration of the follower during return stroke =

 

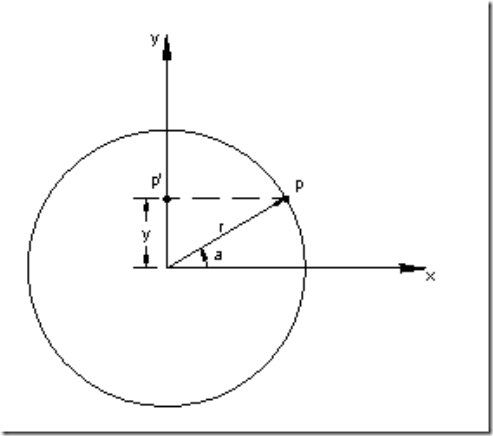
(d) Simple Harmonic Motion: In fig.5, the motion executed by point P^l, which is the projection of point P on the vertical diameter is called simple harmonic motion. Here, P moves with uniform angular velocity ω_p, along a circle of radius r (r = s/2).

Fig.5: Simple Harmonic Motion

Displacement = ; [d1]

Velocity = ; [d2]

Acceleration = ; [d3]

Fig.6: Follower Displacement Diagram with Simple Harmonic Motion

s= Stroke or displacement of the follower.

θ_o = Angular displacement during outstroke.

θ_r = Angular displacement during return stroke

ω = Angular velocity of cam.

t_o = Time taken for outstroke =

t_r = Time taken for return stroke =

Max. velocity of follower during outstroke = vo_max = rω_p (from d2)

 

vo_max =

Similarly Max. velocity of follower during return stroke = , vr_max =

 

Max. acceleration during outstroke = ao_max = rω²_p (from d3) =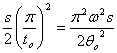

 

Similarly, Max. acceleration during return stroke = ar_max =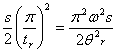

 

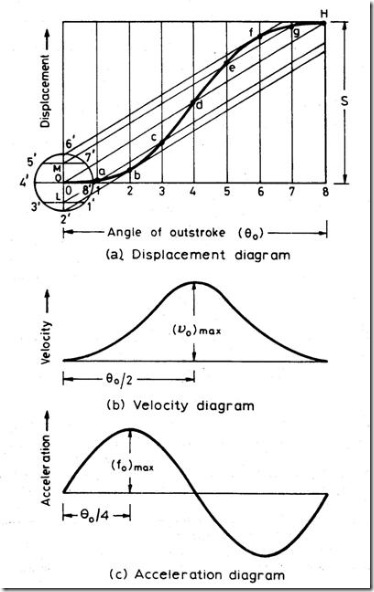
(e) Cycloidal motion:

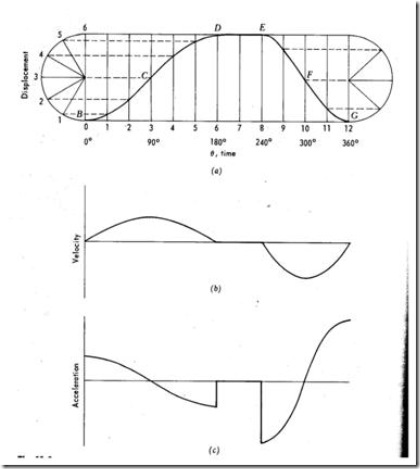
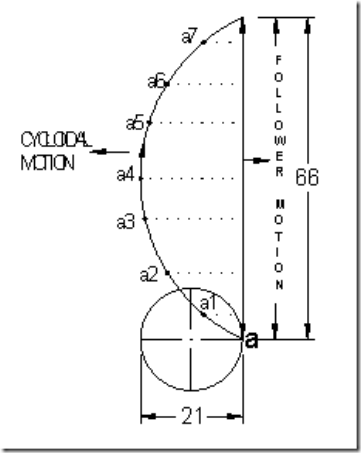
Cycloid is the path generated by a point on the circumference of a circle, as the circle rolls without slipping, on a straight/flat surface. The motion executed by the follower here, is similar to that of the projection of a point moving along a cyloidal curve on a vertical line as shown in figure 7.

Fig.7: Cycloidal motion

The construction of displacement diagram and the standard patterns of velocity and acceleration diagrams are shown in fig.8. Compared to all other follower motions, cycloidal motion results in smooth operation of the follower.

The expressions for maximum values of velocity and acceleration of the follower are shown below.

s = Stroke or displacement of the follower.

d = dia. of cycloid generating circle =

θ_o = Angular displacement during outstroke.

θ_r = Angular displacement during return stroke

ω = Angular velocity of cam.

t_o = Time taken for outstroke =

t_r = Time taken for return stroke =

vo_max = Max. velocity of follower during outstroke =

vr_max = Max. velocity of follower during return stroke =

ao_max = Max. acceleration during outstroke =

ar_max = Max. acceleration during return stroke =

Fig. 8: Follower Displacement, Velocity & Acceleration Diagram for Cyloidal Motion