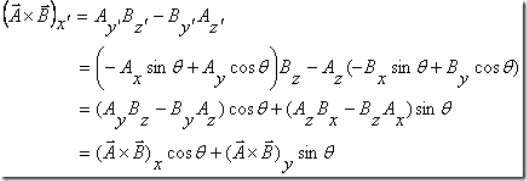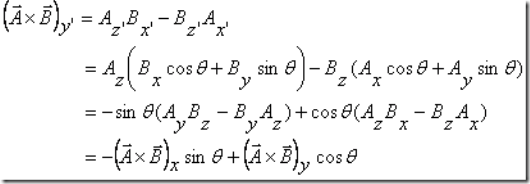Engineering Mechanics | Cross product of two vectors

Vector or cross product: In defining the scalar product above, we have used three out of the nine possible products of the components of two vectors. From the six of these that are left i.e. , if we define the vector

This is known as the vector or cross product of the two vectors. By calling this expression a vector, we implicitly mean that its component transform like those of a vector. Let us again take the example of looking at the components of this quantity from two frames rotated with respect to each other about the z-axis. In that case the x component of the vector product in the rotated frame is

and the y component is

Thus we see that the components of the vector product defined above do indeed transform like those of a vector. We leave it as an exercise to show that when the other frame is obtained by rotating about the x and the y axes also, the transformation of the components is like that of a vector. This is known as the vector or the cross product of vectors and . It can also be written in the form of a determinant as

s

Notice that this is the only contribution that transforms in this manner. For example

does not transform like a vector; I leave it as an exercise for you to show. So this cannot form a vector.

Now if we take the dot product of or with , the result is zero as is easy to see. This implies that the vector product of two vectors is perpendicular to both of them. As such an alternate expression for the vector product of is

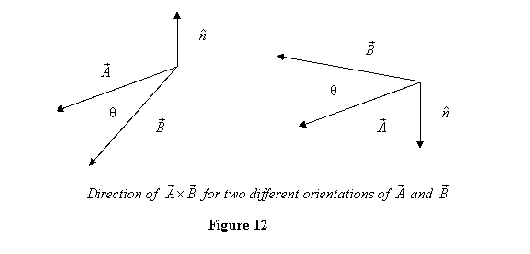
where is a unit vector in the direction perpendicular to the plane formed by in such a way that if the fingers of the right hand turn from to through the smaller of the angle between them, the thumb gives the direction of in direction of . It is also clear from this expression that the vector product of two non-zero vectors will vanish if the vectors are parallel i.e. the angle between them is zero.

The vector product between two vectors is not commutative in that but rather .