STRAIGHT LINE MECHANISMS | Kinematics of Machines Tutorials

STRAIGHT LINE MECHANISMS

Straight line motion mechanisms

Straight line motion mechanisms are mechanisms, having a point that moves along a straight line, or nearly along a straight line, without being guided by a plane surface.

Condition for exact straight line motion:

If point B (fig.1.40) moves on the circumference of a circle with center O and radius OA, then, point C, which is an extension of AB traces a straight line perpendicular to AO, provided product of AB and AC is constant.

Fig.1.40: Condition for exact straight line motion

Locus of pt.C will be a straight line, ┴ to AE if, is constant

Proof:

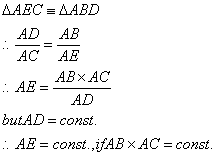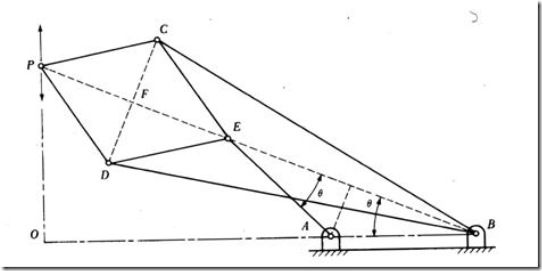
Peaucellier exact straight line motion mechanism:

Fig.1.41: Peaucellier exact straight line motion mechanism

Here, AE is the input link and point E moves along a circular path of radius AE = AB. Also, EC = ED = PC = PD and BC = BD. Point P of the mechanism moves along exact straight line, perpendicular to BA extended.

To prove B, E and P lie on same straight line:

Triangles BCD, ECD and PCD are all isosceles triangles having common base CD and apex points being B, E and P. Therefore points B, E and P always lie on the perpendicular bisector of CD. Hence these three points always lie on the same straight line.

To prove product of BE and BP is constant.

In triangles BFC and PFC,

and

But since BC and PC are constants, product of BP and BE is constant, which is the condition for exact straight line motion. Thus point P always moves along a straight line perpendicular to BA as shown in the fig.1.41.

Approximate straight line motion mechanism: A few four bar mechanisms with certain modifications provide approximate straight line motions.

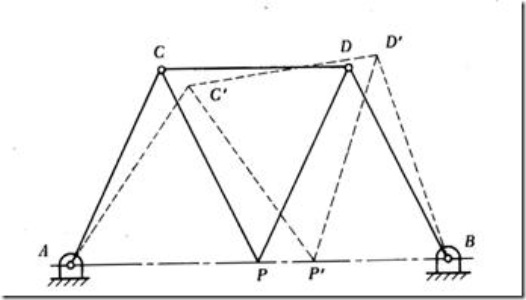
Robert’s mechanism

Fig.1.42: Robert’s mechanism

This is a four bar mechanism, where, PCD is a single integral link. Also, dimensions AC, BD, CP and PD are all equal. Point P of the mechanism moves very nearly along line AB.