STEERING MECHANISMS
Hooke’s joint (Universal joints)
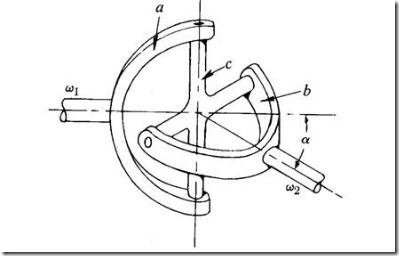
Hooke’s joins is used to connect two nonparallel but intersecting shafts. In its basic shape, it has two U –shaped yokes ‘a’ and ‘b’ and a center block or cross-shaped piece, C. (fig.1.47(a))
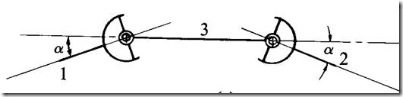
The universal joint can transmit power between two shafts intersecting at around 300 angles (α). However, the angular velocity ratio is not uniform during the cycle of operation. The amount of fluctuation depends on the angle (α) between the two shafts. For uniform transmission of motion, a pair of universal joints should be used (fig.1.47(b)). Intermediate shaft 3 connects input shaft 1 and output shaft 2 with two universal joints. The angle α between 1 and 2 is equal to angle α between 2 and 3. When shaft 1 has uniform rotation, shaft 3 varies in speed; however, this variation is compensated by the universal joint between shafts 2 and 3. One of the important applications of universal joint is in automobiles, where it is used to transmit power from engine to the wheel axle.
Fig.1.47(a)
Fig.1.47(b): Hooke’s joint
Steering gear mechanism
The steering mechanism is used in automobiles for changing the directions of the wheel axles with reference to the chassis, so as to move the automobile in the desired path. Usually, the two back wheels will have a common axis, which is fixed in direction with reference to the chassis and the steering is done by means of front wheels.
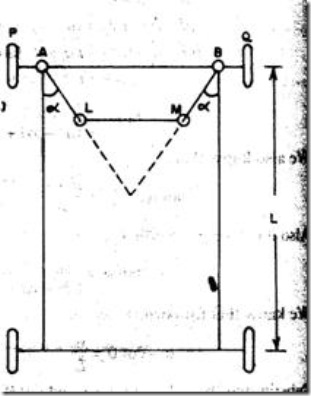
In automobiles, the front wheels are placed over the front axles (stub axles), which are pivoted at the points A & B as shown in the fig.1.48. When the vehicle takes a turn, the front wheels, along with the stub axles turn about the pivoted points. The back axle and the back wheels remain straight.
Always there should be absolute rolling contact between the wheels and the road surface. Any sliding motion will cause wear of tyres. When a vehicle is taking turn, absolute rolling motion of the wheels on the road surface is possible, only if all the wheels describe concentric circles. Therefore, the two front wheels must turn about the same instantaneous centre I which lies on the axis of the back wheel.
Condition for perfect steering
The condition for perfect steering is that all the four wheels must turn about the same instantaneous centre. While negotiating a curve, the inner wheel makes a larger turning angle θ than the angle φ subtended by the axis of the outer wheel.
In the fig.1.48, a = wheel track, L = wheel base, w = distance between the pivots of front axles.
Fig.1.48: Condition for perfect steering
![]() . This is the fundamental equation for correct steering. If this condition is satisfied, there will be no skidding of the wheels when the vehicle takes a turn.
. This is the fundamental equation for correct steering. If this condition is satisfied, there will be no skidding of the wheels when the vehicle takes a turn.
Ackermann steering gear mechanism
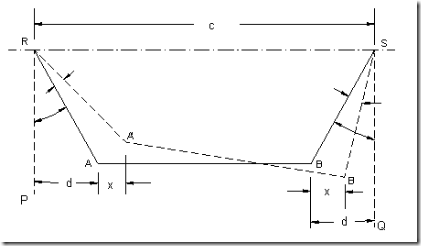
Fig.1.49: Ackermann steering gear mechanism
fig.1.50: Ackermann steering gear mechanism
Ackerman steering mechanism, RSAB is a four bar chain as shown in fig.1.50. Links RA and SB which are equal in length are integral with the stub axles. These links are connected with each other through track rod AB. When the vehicle is in straight ahead position, links RA and SB make equal angles α with the center line of the vehicle. The dotted lines in fig.1.50 indicate the position of the mechanism when the vehicle is turning left.
Let AB=l, RA=SB=r; ![]() and in the turned position,
and in the turned position, ![]() . IE, the stub axles of inner and outer wheels turn by θ and φ angles respectively.
. IE, the stub axles of inner and outer wheels turn by θ and φ angles respectively.
Neglecting the obliquity of the track rod in the turned position, the movements of A and B in the horizontal direction may be taken to be same (x).
Angle α can be determined using the above equation. The values of θ and φ to be taken in this equation are those found for correct steering using the equation ![]() . [2]
. [2]
This mechanism gives correct steering in only three positions. One, when θ = 0 and other two each corresponding to the turn to right or left (at a fixed turning angle, as determined by equation [1]).
The correct values of φ, [φc] corresponding to different values of θ, for correct steering can be determined using equation [2]. For the given dimensions of the mechanism, actual values of φ, [φa] can be obtained for different values of θ. T he difference between φc and φa will be very small for small angles of θ, but the difference will be substantial, for larger values of θ. Such a difference will reduce the life of tyres because of greater wear on account of slipping.
But for larger values of θ, the automobile must take a sharp turn; hence is will be moving at a slow speed. At low speeds, wear of the tyres is less. Therefore, the greater difference between φc and φa larger values of θ ill not matter.
As this mechanism employs only turning pairs, friction and wear in the mechanism will be less. Hence its maintenance will be easier and is commonly employed in automobiles.

7 Responses to “STEERING MECHANISMS | Kinematics of Machines Tutorials”
amit kumar
it is very good site.it give detail knowledge in very simple way.
Ahmed
Please explain in detail in a vidwo
admin
Sure. Will Try.
Anyway, thanks for the comment.
Aiman Ur Rahman
I need a PDF of Steering gears
Manish
Xcuse can you pls tell me how can we find the ae distance.
Mohan reddy
I need grasshoppers
GooRaT
i get it now 🙂