Engineering Mechanics | Derivative of a vector

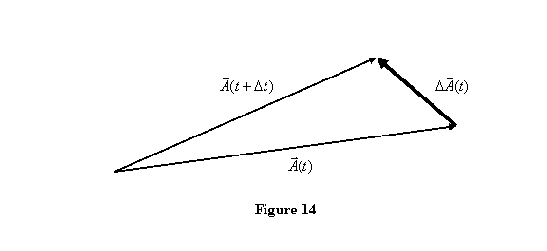
Derivative of a vector: After reviewing the vector algebra, we would now like to introduce you to the idea of differentiating a vector quantity. Here we take a vector as depending on one parameter, say time t , and evaluate the derivative . This is similar to what we do for a regular function. We evaluate the vector at time (t+ Δt) , subtract from it, divide the difference by Δt and then take the limit Δ t → 0 .

This is shown in figure 14. Thus

The derivative is easily understood if we think in terms of its derivatives. If we write a vector as

then the derivative of the vector is given as

Notice that only the components are differentiated, because the unit vectors are fixed in space and therefore do not change with time. Later when we learn about polar coordinates, we will encounter unit vectors which also change with time. In that case when taking derivative of a vector, the components as well as the unit vectors both have to be differentiated.

Using the definition above, it is easy to show that in differentiating the product of two vectors, the usual chain rule can be applied. This gives

and

This pretty much sums up our introduction to vectors. I leave this lecture by giving you three exercises.

1. Show that and that is the volume of a parallelepiped formed by .

2. Show that can also be written as the determinant